The Late Holocene Dry Period (LHDP) and the Medieval Climatic Anomaly (MCA) in the Northern Great Basin
A Bayesian Non-Parametric View
(This is a slightly updated version of my talk at the 50th Idaho Archaeology Society Conference in Boise this past October. Comments welcome as I work on getting this more formally written up!)
Morning, Mark Hall here. This short talk is arising from a project that Ian Hutchison (Simon Fraser University) and I started before the COVID-19 pandemic. As with a lot of things, it got off-track during the pandemic and only recently have we picked it back up. And in addition to acknowledging Ian’s contribution at getting this radiocarbon database developed, I also need to acknowledge the help of Emma Vance of the BLM (now an archaeologist with the Oregon Dept. of Transportation) in collecting some of the reports that added more radiocarbon dates to this project.
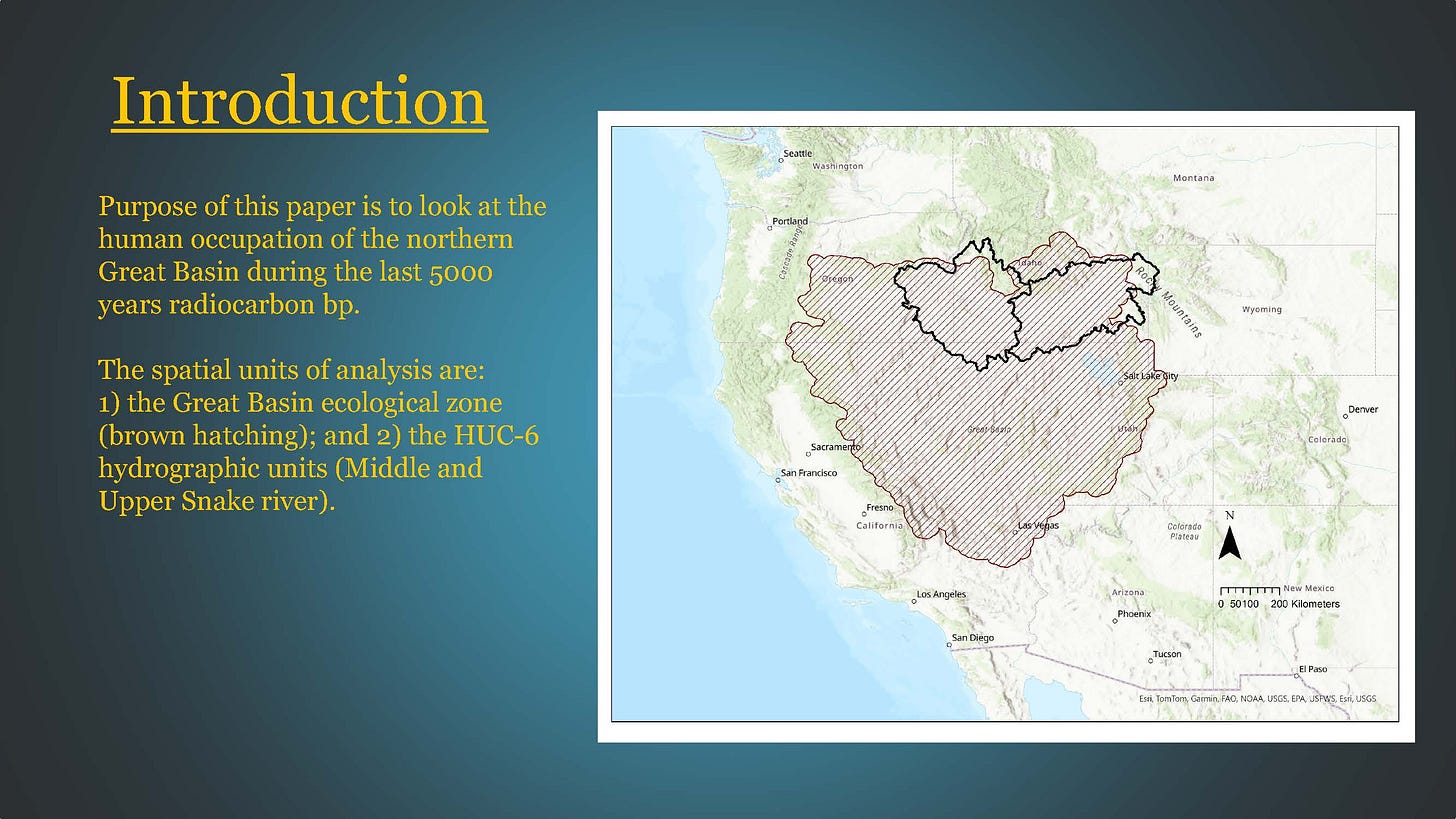
The purpose of this paper is to look at human use of the Northern Great Basin over the last 5000 radiocarbon years. The geographic unit of analysis for this study is the Northern Great Basin as defined by Dept. of Interior’s ecological habitat intersecting with the US Geological Survey hydrographic basins.
The hydrographic basin unit under examination is at the HUC-6 level. The HUC system was devised by USGS in 1994 (Seaber et. al. 1987). The HUC-6 unit is a designated hydrographic accounting unit containing the area drained by a given river, its tributaries, and any closed basins (Seaber et. al. 1994:3). Looking at the Upper and Middle Snake HUC-6 units.
This is a work in progress, though I feel there are enough radiocarbon dates to at least show the trends in the data.
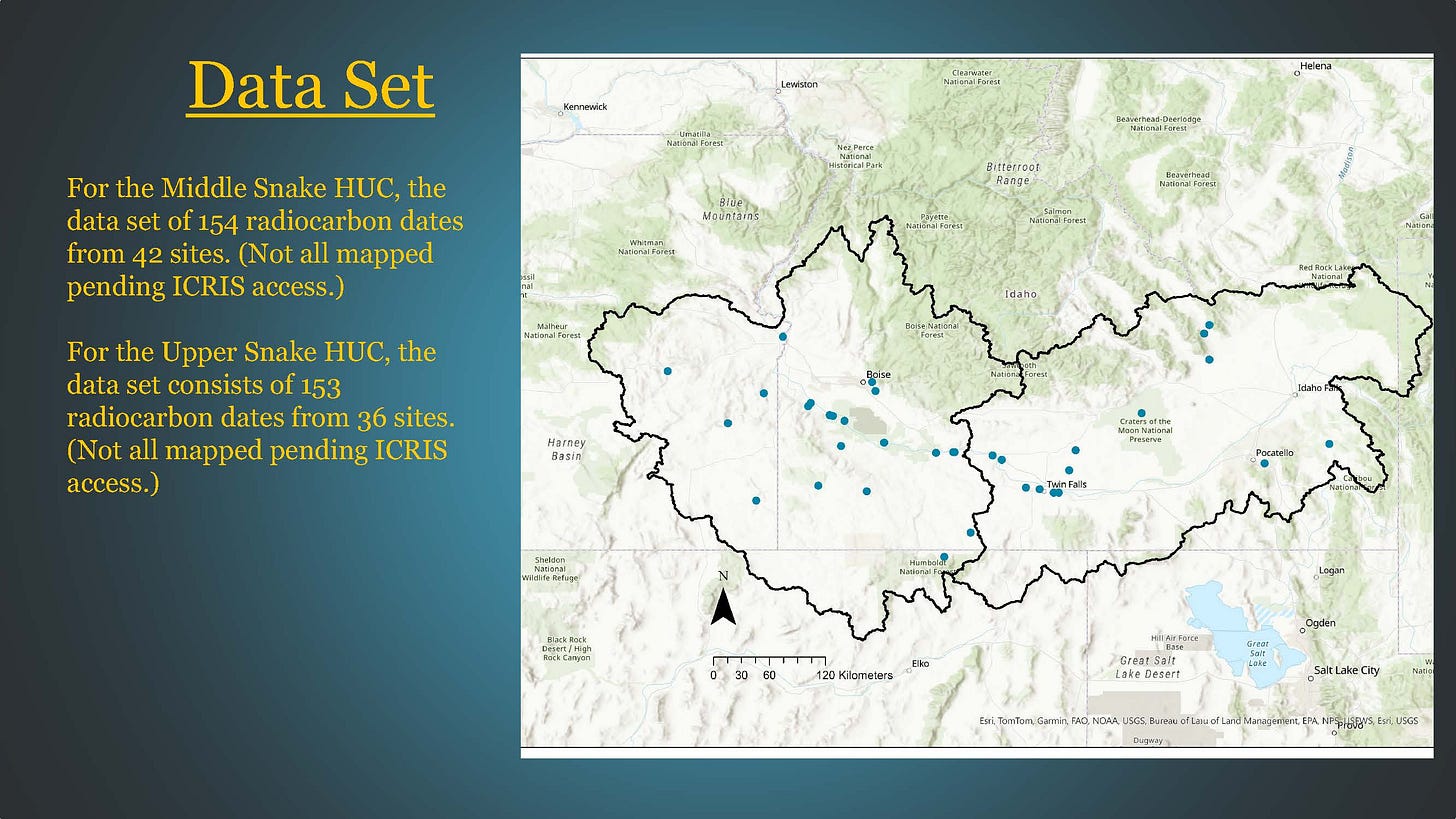
This slide shows a partial map of the sites contributing dates to this study. Not all the sites are shown; I need to work on getting access to ICRIS for the rest of the spatial data.
For the Middle Snake River Hydrographic basin, the radiocarbon database currently consists of 154 radiocarbon dates from 42 sites. 21 dates are from the Birch Creek site in Malheur County, 16 dates are from the Givens Hot Springs site, and 13 dates are from Dirty Shame rockshelter. The other sites contribute anywhere from one to five dates respectively.
The radiocarbon database for the Upper Snake River Hydrographic basin contains 153 radiocarbon dates from 36 sites. 19 dates are from Veratic rockshelter, 16 dates are from Bison rockshelter, and 12 dates from Alpha Cave.
All dates used in this study are from human modified materials (including hearths), human and animal remains. Soil humic fractions are not part of the database. No shell dates are included. All dates also have a radiocarbon lab number.
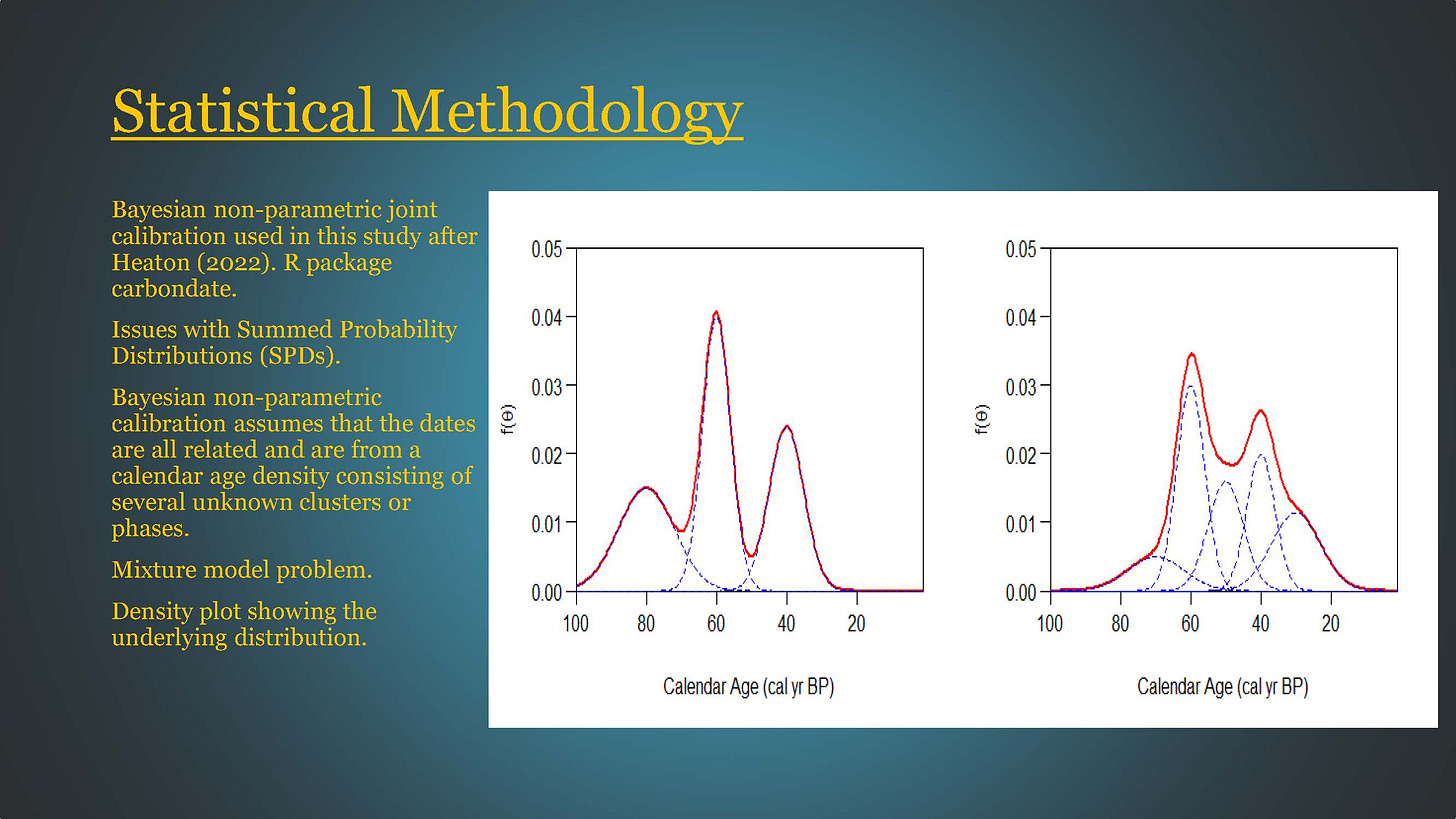
Bayesian non-parametric calibration is the methodology employed here as developed by Heaton (2022).
SPDs are the way summary calibrated dates are presented. They are essentially the summation of the individually calibrated dates. Issues with SPDs:
1) uncertainty in the calibration curve can confound the calibration process; and
2) SPDs conflate the number of events with the uncertainty of their temporal positions—there is no connection to the number of events that occurred in the interval of an SPD to its height. (Note: height influenced by the curve shape.)
SPDs are only readily suited for an integral approach which looks at changes through time by the area under the SPD.
Bayesian non-parametric calibration assumes that the dates are all related and are from a calendar age density consisting of a number of unknown clusters or phases. The calendar age density can be decomposed into several normal distributions with a mean and standard deviation within overall density.
This is essentially a mixture model problem which has been dealt with for decades by frequentists and Bayesians.
Bayesian calibration of radiocarbon dates typically involves updating prior information (such as prior distributions for calendar ages) using likelihood functions based on radiocarbon data. The outcome is a posterior distribution for the calendar age of a sample.
Non-parametric aspect: Unlike parametric methods, which assume a specific form for the underlying distribution of calendar ages, Heaton’s approach does not make strict assumptions about the form of the calibration curve. This allows for more flexibility in capturing complex features of the data.
The calibration process involves the following major steps:
Set the model: Assume a prior distribution for the unknown calendar ages and a likelihood function for the observed radiocarbon dates. The goal is to sample from the posterior distribution of the calendar ages, given the radiocarbon dates and the calibration curve.
Initial cluster formation:
A key part of the non-parametric approach is to allow data points (radiocarbon dates) to cluster in an adaptive way.
Clustering is often initiated using a Dirichlet Process (DP) prior, which enables the formation of an unknown number of clusters, where each cluster corresponds to a different region of the calibration curve.
Sampling using MCMC: Since exact solutions to the Bayesian posterior distribution are usually intractable, Markov Chain Monte Carlo (MCMC) methods are used to approximate the posterior.
The MCMC samplers employed in Heaton’s Bayesian non-parametric approach include:
Pólya Urn Scheme: This is a technique for generating samples from a Dirichlet Process. Each new observation is either assigned to an existing cluster with probability proportional to the number of observations already in that cluster or is assigned to a new cluster.
Pólya urn algorithm is key for data-driven clustering. As new radiocarbon samples are added, they are allocated either to an existing cluster (an existing region of the calibration curve) or to a new cluster, based on the prior and the current state of the system.
Walker’s Slice Sampler: This is used for efficient sampling from the posterior distribution. It is particularly effective for hierarchical models like those arising in Dirichlet Process-based methods.
Slice sampling works by introducing an auxiliary variable to simplify sampling from the posterior distribution. In the case of the Dirichlet Process, the Walker Slice Sampler allows efficient sampling from the infinite-dimensional distribution that governs the clusters of radiocarbon data.
In Heaton's non-parametric Bayesian framework, clustering of the radiocarbon dates occurs naturally through the Dirichlet Process.
Cluster formation:
Initially, each radiocarbon date may be considered as its own cluster.
As the MCMC algorithm proceeds, dates that are close to each other (in terms of calendar age or radiocarbon measurement) are more likely to be grouped into the same cluster.
The clustering process is adaptive, meaning that the number and size of clusters are not fixed but determined by the data.
This clustering enables the model to adapt to different regions of the calibration curve, which may have different levels of uncertainty or complexity.
Bayesian models require specifying priors for the unknown parameters. In Heaton’s approach employs 3 priors:
Dirichlet Process Prior: The non-parametric nature of the model relies on a Dirichlet Process prior, which governs how the clusters of calendar ages are formed. The concentration parameter of the Dirichlet Process controls the probability of creating new clusters:
A higher concentration parameter leads to more clusters (i.e., the data are more likely to be split into many small clusters).
A lower concentration parameter results in fewer, larger clusters (i.e., more smoothing over the calibration curve).
Calendar age priors: Priors for the calendar ages are often chosen based on historical or archaeological context. These can be uninformative (allowing the data to dominate the inference) or informative (based on prior knowledge about the likely calendar ages).
Priors for radiocarbon data: Radiocarbon dating uncertainties (measured as standard deviations of radiocarbon dates) are typically incorporated into the likelihood function. This ensures that the uncertainty in the radiocarbon measurement is propagated into the calendar age estimates.
A summary of Heaton’s algorithm is as follows:
Define the model: Choose a prior distribution for calendar ages and a likelihood based on radiocarbon dates.
Initialize clusters: Use a Dirichlet Process prior to allow for flexible clustering of radiocarbon dates.
Sample from the posterior: Use MCMC methods, including the Pólya Urn scheme and Walker Slice Sampler, to sample from the posterior distribution of the calendar ages.
Update clusters: As more data are considered, the clustering of radiocarbon dates evolves adaptively.
Obtain posterior estimates: After running the MCMC chain, obtain posterior distributions for the calendar ages and corresponding credible intervals.
The results of the calibration process are a predictive density curve summarizing the calendar dates of the radiocarbon determinations.
Need to realize it is possible that the radiocarbon determinations could come from a distribution that is poorly represented by a sum of normal mixture model. Need to check MCMC statistics, and looking at CKDE or RECE models also useful. Reality is often messy, but normal models are handy tools to clean up the mess.
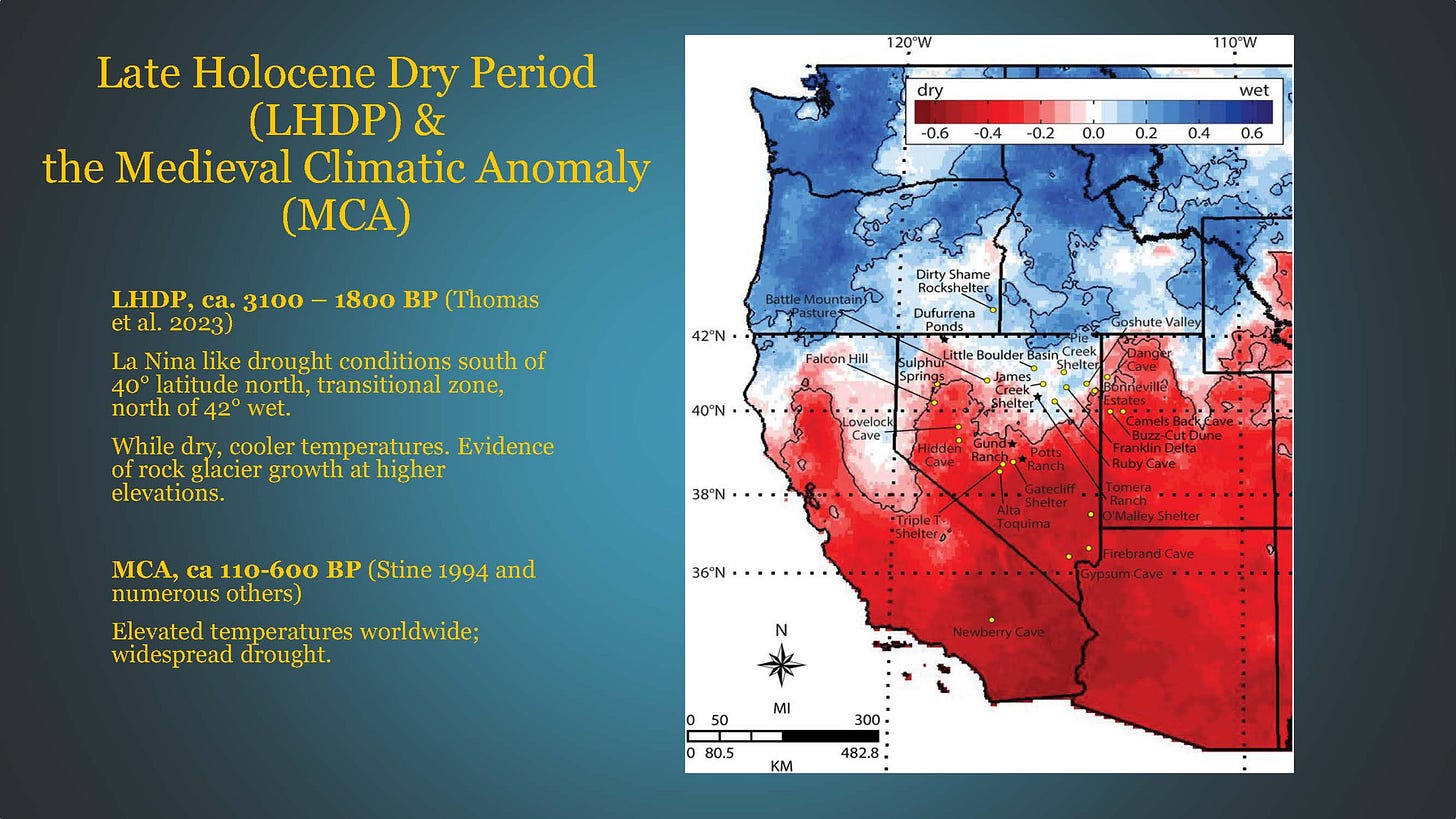
The climatic phases focused on in this study are the Late Holocene Dry Period (LHDP), ca. 3100-1800 BP (Thomas 2023) and the Medieval Climatic Anomaly (MCA) ca. 1100-600 BP (Stine 1994).
The LHDP is characterized by a severe drought in Central and Southern NV, a transitional zone between 40 degrees and 42 degrees North latitude. North of 42 degrees latitude is seen as being wet. South of 40 degrees north, abandonment of the lowlands, shift to some upper altitudes for settlement.
While the LHDP is a drought, temperatures are considered cooler and at the start of it there is the growth of glaciers in a variety of mountain ranges implying cooler temperatures.
The MCA was a worldwide phenomenon of elevated global temperatures believed by some to be due to increased solar radiation and a decrease in volcanic activity. Large parts of the great Basin are seen as being very dry, while the PNW is seen as being wet. The Northern Great Basin is a transitional zone between climatic regimes.
While I’ve given an overview of the climatic trends, there are three sites yielding pollen data that can be used to reconstruct the palaeoclimate. The LegacyClimate 1.0 dataset (Herzschuh et al. 2023) uses the Modern Analogue Technique to reconstruct climatic variables from a standardized set of pollen data from almost 3000 sites in North America.
One caveat about the data set, the calendar ages are from the raw calibration of the radiocarbon dates and using the median calibrated date. In my opinion, I think a Bayesian methodology needs to be employed and the maximum-a-priori calibrated date reported.
For Lake Cleveland, the pollen data is suggestive of a slight decline in precipitation in both the LHDP and the MCA (figure above).
For the Middle Snake River HUC, the 1984 Mission Cross Bog core shows an overall decrease in precipitation from the start to the end of the LHDP. For the MCA, precipitation increase throughout the period. (It bears noting there are two other Mission Cross Bog cores and where they do overlap they tell very different stories. More work is needed to harmonize the data sets.)
The Van Wyck core data indicates that precipitation fluctuated throughout the LHDP, and generally decreased during the MCA.
General note on the calibration results: There were one million iterations for all MCMC calculations with a thinning of ten iterations, and a burn-in of 50,000 iterations.
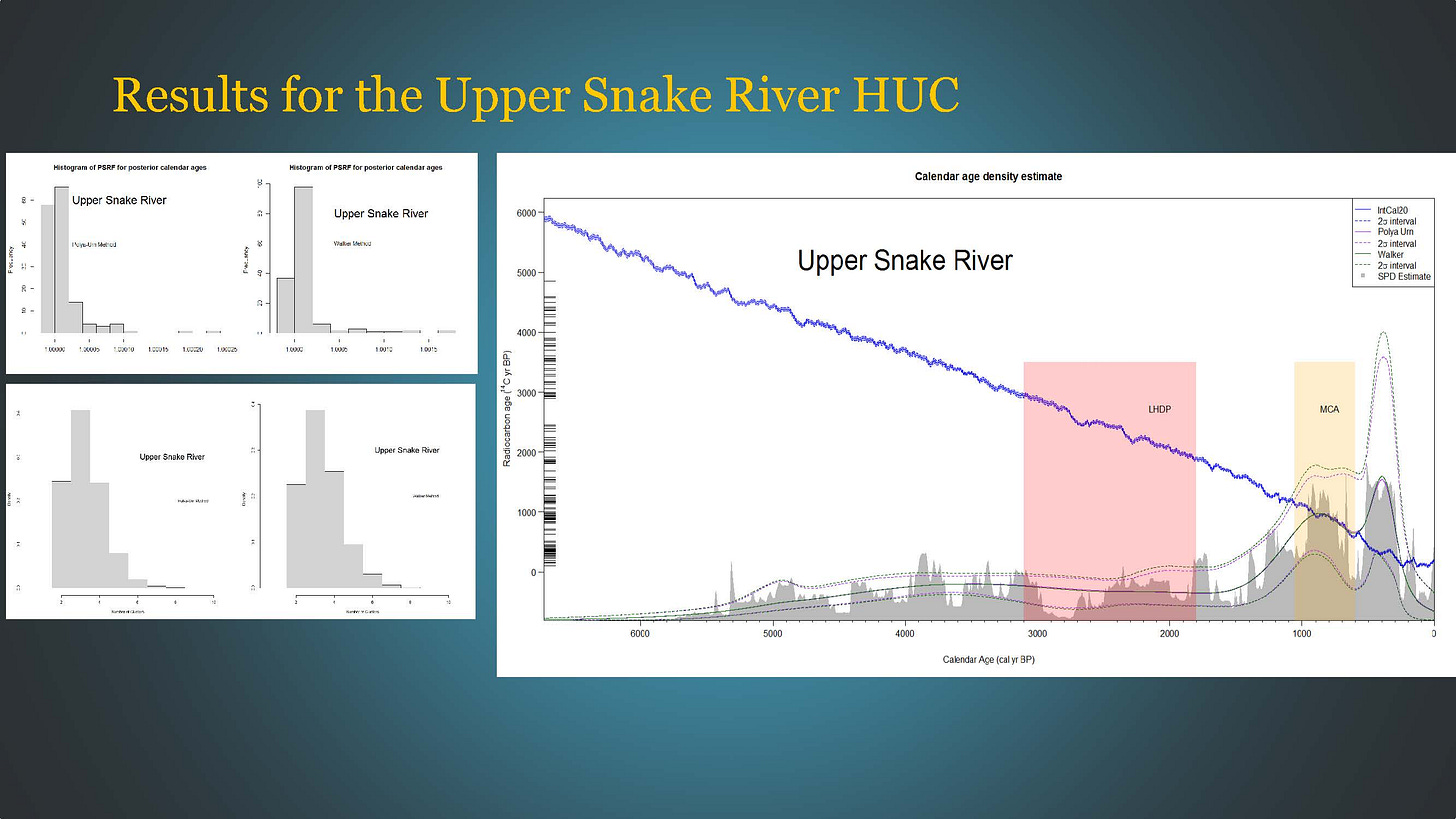
Upper Snake River results—
Convergence based on the Gelman-Rubin statistic.
3 clusters are the dominant model. Centered at 4950 BP, 900 BP, and 400 BP.
During the LHDP, a low but constant level of human activity in the hydrographic unit. During the MCA a slight decline, but overall holding constant. The decline in the MCA coincides with the decline in precipitation.
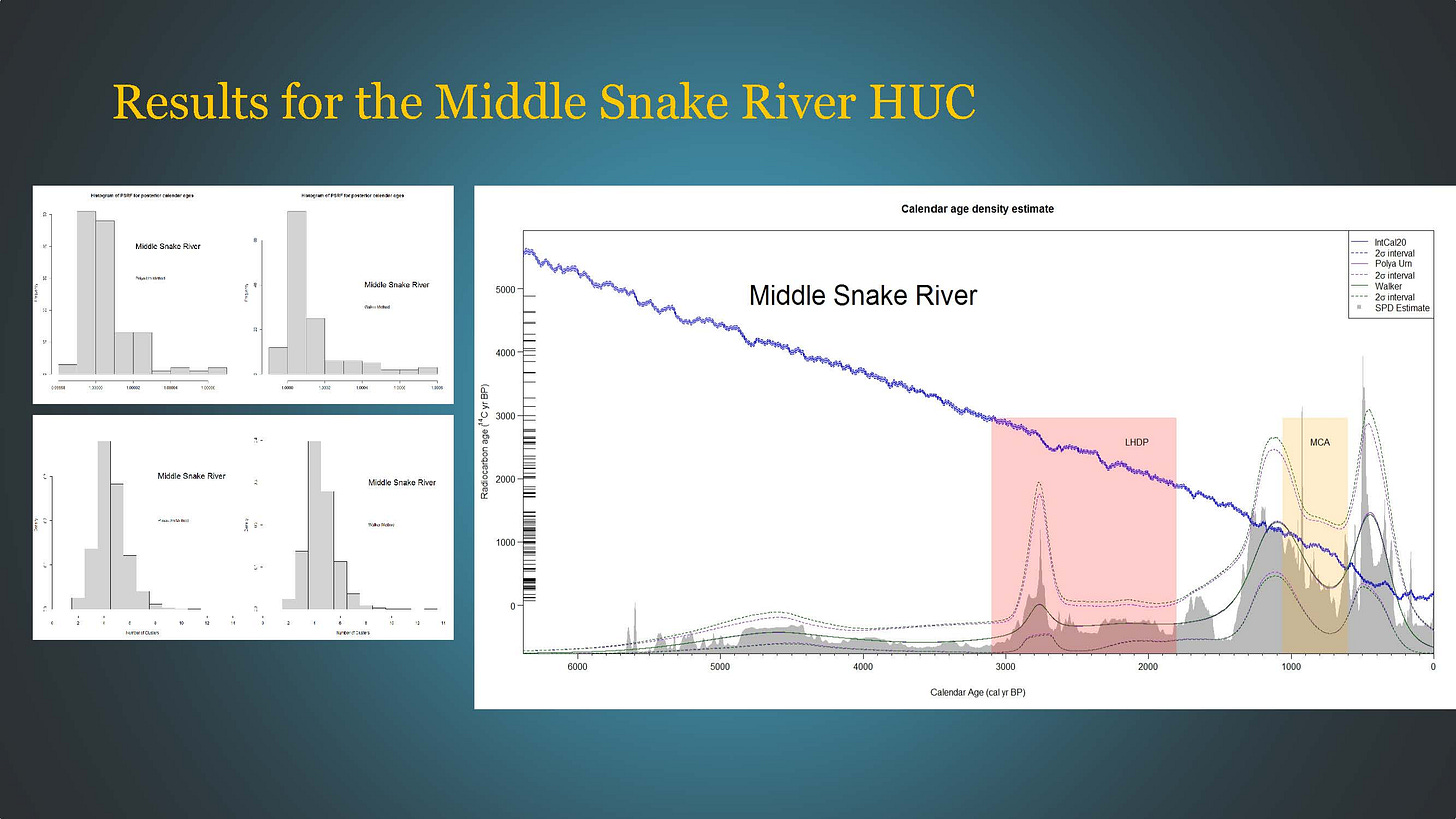
Middle Snake River results—
Convergence based on the Gelman-Rubin statistic.
4 clusters are the dominant mode. Centered at 4400 BP, 2800 BP, 1150 BP, and 400 BP.
During the LHDP, there is a sharp increase in human activity and then a sudden decrease to a low level throughout the rest of the LHDP. This coincides with the precipitation decline seen in the Mission Cross Bog pollen core.
In the MCA, the is a continuing decrease in human activity throughout the climatic phase.
In conclusion, a more focused study looking at various drainages in the Great Basin show the variation in how humans responded to major climatic events. A “business as usual model” for 42 degrees latitude and north does not hold true during the LHDP—the Middle Snake river basin sees a collapse in human activity, while the Upper Snake river has a low-level constant activity. For the MCA a similar pattern of collapse and constancy is seen.
References:
Heaton, T.J., 2022. Non-parametric calibration of multiple related radiocarbon determinations and their calendar age summarisation. Journal of the Royal Statistical Society Series C: Applied Statistics, 71(5), pp.1918-1956.
Seaber, P.R., Kapinos, F.P. and Knapp, G.L., 1987. Hydrologic Unit Maps: US Geological Survey Water-Supply Paper 2294 (USGS, Reston, VA).
Stine, S., 1994. Extreme and persistent drought in California and Patagonia during mediaeval time. Nature, 369(6481), pp.546-549.
Thomas, D.H., Rhode, D., Millar, C.I., Kennett, D.J., Harper, T.K. and Mensing, S., 2023. Great Basin Survivance (USA): Challenges and Windfalls of the Neoglaciation/Late Holocene Dry Period (3100–1800 cal BP). American Antiquity, 88(3), pp.402-418.